卷上 第 1a 页 WYG0220-0695c.png
钦定四库全书
琴旨卷上
南通州王坦撰
五声数论琴
夫古人审定八音之乐各从其类匏竹以度之长短较
其空窍各均土以量之多寡较其中空容受金石以权
衡之轻重较其厚薄等差革本止一声为众乐之节奏
其体制大小悉以律吕为准则至于丝则丝纶有巨细
徽柱有长短必以五声之数较定之方不失古圣人作
卷上 第 1b 页 WYG0220-0695d.png
乐精微之妙后世以丝竹之乐为八音之要领竹乐以
律吕相较丝乐亦以律吕相较有谓黄钟均以仲吕为
角此以律吕论琴不得其所以然之理也有谓隋废旋
宫独存黄钟一均此以律吕论琴并失旋宫之义也或
以律吕名调(以徵调为蕤宾调以商调为姑洗调是也)(或以律吕名
弦 宋姜 夔七 )
(弦琴图说黄钟大吕并用慢角调故于大弦十一徽应三弦散声云云
是也 或以律吕名徽)
(明张右衮太古琴经以十二徽象十二月中之第七徽象闰是也)(纷
纷聚讼讫无定说)
卷上 第 2a 页 WYG0220-0696a.png
孟子曰不以六律不能正五音盖以六律六吕三分损
益隔八相生之理正此五音也何尝以六律六吕为此
调此弦此徽之本乎盖竹乐管音其体本虚故围径之
大小空窍之长短可较以十二律吕之度以某律吕之
度定其围径大小之度为之体以某律吕某律吕之度
定其空窍长短之度为之用若丝乐弦音其体本实故
丝纶巨细得数之多寡徽分长短得数之疏密
(独论琴故曰徽分巨弦数多者分密细弦数少者分疏故曰得数之疏
密 则必较以五声之)
数以某声之数定其丝纶多寡之数为之体以某声某
卷上 第 2b 页 WYG0220-0696b.png
声之数定其徽分疏密之数为之用此律吕之度较管
音五声之数较弦音一定之理也琴虽七弦止有宫商
角徵羽五正声得为用巨弦数多以五声数之多者主
之细弦数少以五声数之少者主之乌可以黄钟之九
寸太蔟之八寸为准则耶自古原以五声数论弦音故
相传有宫商角徵羽少宫少商七弦之名弦数多寡既
以五声数为准则而徽分疏密得声之应和亦当以五
卷上 第 3a 页 WYG0220-0696c.png
声数较之其理自明矣夫黄钟九寸之声宫声八十一
之数二者相为表里而损益相生其声原无不协故唐
宋而后遂执律吕之度以论弦音殊不知管音与弦音
秉质有虚实之异生声取分不能相同管音全度无论
长短全半不相应(箫笛自吹口至第一孔之度九寸为全度至第六孔
之度四寸五分为半 )
(度而声低一字不相应必于四寸之度声相应是无论长短全半不相
应也 弦音全度无论)
长短全半相应(焦尾至岳山为全度七徽为半度而声相应七徽至岳
山为全度四徽为半度 )
(而声相应四徽至岳山为全度一徽为半度而声相应是无论长短全
半相应也 管音自首音)
至第八音七声相均俱得全分得七全分
卷上 第 3b 页 WYG0220-0696d.png
(度声低一字阳律黄钟宫得黄钟之半为变宫阴吕大吕清宫得大吕
之半为凊变宫阳律以黄钟为宫太蔟 )
(为商姑洗为角蕤宾为变徵夷则为徵无射为羽半黄钟为变宫半太
蔟仍为宫阴吕大吕为宫夹钟为商仲 )
(吕为角林钟为变徵南吕为徵应钟为羽半大吕为变宫半夹钟仍为
宫阳律得半律而为七阴吕亦得半吕 )
(而为七故七声相均得七全分也)(弦音自首音至第八音七声不相
均)
止得五全分二半分实得六全分(弦音之七声不相均者因止用五正
声变 )
(宫至宫得半分变徵至徵亦得半分而不得为用故止得五全分二半
分为六全分也 是故管律)
与徽分欲取其声之同则其分不同欲取其分之同则
卷上 第 4a 页 WYG0220-0697a.png
生声不同若以管音考覈弦音非理数之自然无由得
贯通之妙黄帝作八音伶伦截竹为管葭莩为灰以仲
冬之月气至灰动为黄钟之管得黍九十为九寸即宫
声之八十一也(侯气之法为室三重户闭涂衅必周密布缇缦室中以
木为案每律吕一内庳 )
(外高从其方位加律其上以葭莩灰抑其内端案律而候之其为气所
动者灰散人及风所动者灰聚 用)
三分损益隔八相生之法损而下生益而上生终于仲
吕得律十二以配十有二月而度量权衡之理生焉黄
钟之长九十黍为分寸尺丈引曰度以较匏竹之音黄
钟之容千二百黍为龠合升斗斛曰量以较土乐之音
卷上 第 4b 页 WYG0220-0697b.png
黄钟所容千二百黍之重为铢两斤钧石曰权衡以较
金石之音因五声之数之取声无迹可见
(行具有五行斯有五声五色五味即万物莫逃乎五矣但色味皆有迹
可推惟声无迹而清浊高下即五声之 )
故用律吕相生之理而众乐之长短多寡轻重
皆得其指归丝乐之取声虽与律吕之理相通若覈其
至要用五声相生之理最为简便(丝纶巨细本具五声自然之理故琴
制自 )
(庖羲也八音之乐制自黄帝以五声无迹可推故用度量权衡之理推
之也古人以五声之数较丝乐不益信 )
卷上 第 5a 页 WYG0220-0697c.png
丝乐之较以五声而不用律吕犹之众乐较以律吕
而不用五声故古人审定八音之乐各从其类也今以
五声相生十二律吕隔八相生管音得十二律吕之长
短俱表图于后可见古圣人较丝乐弦音必以五声之
数不以律吕管音之度取分也
卷上 第 5b 页 WYG0220-0697d.png
卷上 第 6a 页 WYG0220-0698a.png
自宫之八十一损益相生至角之六十四得数皆无奇
零故曰始于宫终于角苟不拘以某数损益相生皆不
能生宫之八十一是始于宫而宫为声之君也角之六
十四损益相生得四十二六六为变宫有奇零不能得
声之正是终于角而声之止于五故谓五正声也盖五
声无迹惟数可以推之欲知其数之得声惟弦音可以
推之宫商角徵羽大小之伦即丝纶巨细之次第也宫
商角徵羽相生之序即弦音隔一下生隔二上生得声
相和之理也
卷上 第 6b 页 WYG0220-0698b.png
卷上 第 7a 页 WYG0220-0698c.png
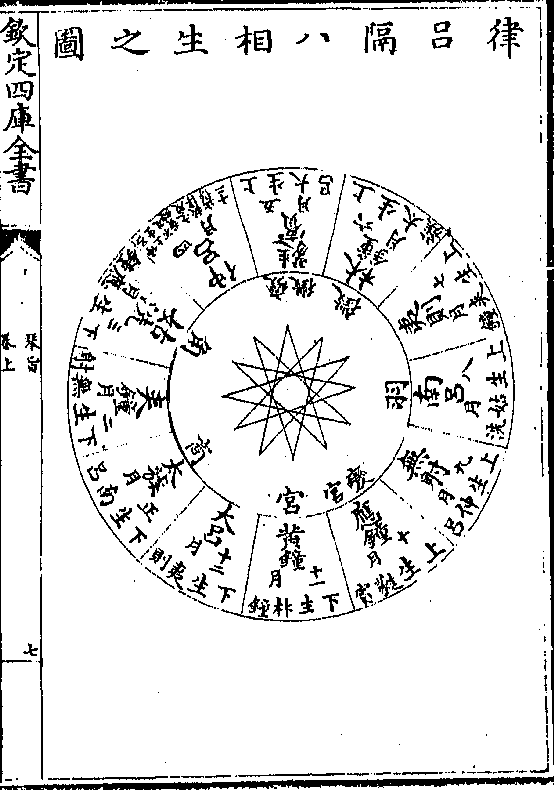
隔八相生始于黄钟终于仲吕得律十二以配十有二
卷上 第 7b 页 WYG0220-0698d.png
月弦音之五声二变运于其中无毫釐之差故唐宋而
后执律吕论琴殊不知生声取分不同也
卷上 第 8a 页 WYG0220-0699a.png
管音自林钟而上俱不与律吕隔八相生之理相合要
卷上 第 8b 页 WYG0220-0699b.png
知不相合乃声音自然之理阴阳分用之妙黄钟宫生
夷则徵夷则徵生太蔟商太蔟商生无射羽无射羽生
姑洗角姑洗角生半黄钟变宫半黄钟变宫生蕤宾变
徵五声二变皆阳也大吕宫生南吕徵南吕徵生夹钟
商夹钟商生应钟羽应钟羽生仲吕角仲吕角生半大
吕变宫半大吕变宫生林钟变徵五声二变皆阴也黄
钟大吕俱得其半度之声为变宫而阳律不及于阴吕
卷上 第 9a 页 WYG0220-0699c.png
阴吕不及于阳律各得一均之七声为一十有四故不
与十二律吕之度相同亦不与弦音之取分相同也
一弦尚徵
一弦为宫世传其说久矣盖缘国语大不踰宫细不过
羽之论也后世以此二语推之遂谓二弦为商三弦为
角四弦为徵五弦为羽六弦应一弦为少宫七弦应二
弦为少商其说虽近自然而不知实失古人作乐之旨
夫大不踰宫宫之前不可定为徵羽则细不过羽羽之
后顾可定为宫商耶何为羽之后又有少宫少商也或
卷上 第 9b 页 WYG0220-0699d.png
谓此亦国语宫逐羽音之说则又不然六弦之宫逐五
弦之羽宁三弦之宫不可逐二弦之羽乎国语自论铸
钟之义非论琴之七弦也(按国语周景王将铸无射之大林伶州鸠对
以云云 自)
隋废旋宫乐经既失世人皆知黄钟宫声为律吕之本
一弦为众弦起音之始故首推一弦为宫声于细按五
音相生之序三分损益之法而一弦尚徵焉宫生徵徵
生商商生羽羽生角宫损一分上生生徵益一分下生
卷上 第 10a 页 WYG0220-0700a.png
亦生徵宫之八十一三分之而损一分则为五十四乃
徵声之数徵之五十四三分之而益一分则为七十二
乃商声之数商之七十二三分之而损一分则为四十
八乃羽声之数羽之四十八三分之而益一分则为六
十四乃角声之数又加宫之八十一三分之而益一分
则为一百有八乃徵声之倍数倍徵之一百有八三分
之而损一分则仍为七十二亦是商声之数商之七十
二三分之而益一分则为九十六乃羽声之倍数倍羽
之九十六三分之而损一分则仍为六十四亦是角声
卷上 第 10b 页 WYG0220-0700b.png
之数按相生之音五而相生之数七宫为八十一商为
七十二角为六十四徵为五十四羽为四十八徵数五
十四倍之为一百有八羽数四十八倍之为九十六古
圣立法上下相生损益并用故琴弦一定有七也倍徵
一百有八纶为一弦(三茧一丝以十二丝为一纶过此则粗不及则细
倍羽九)
十六纶为二弦宫八十一纶为三弦商七十二纶为四
弦角六十四纶为五弦徵五十四纶为六弦羽四十八
卷上 第 11a 页 WYG0220-0700c.png
纶为七弦此依弦之巨细合五声数而为之次第者也
以三弦宫益之而生一弦倍徵一弦倍徵损
之而生四弦商四弦商益之而生二弦倍羽
(此亦隔一下生之理)二弦倍羽损之而生五弦角(此亦隔二上生
之理 五音相 )
(生至角而终角不能生正声也故琴止得五声为用)(此三弦宫声益
而下生得第)
一弦至第五弦又以三弦宫损之而生六弦徵
(理)六弦徵益之亦生四弦商(此隔一下生之理)(四弦商损之
而)
生七弦羽(此亦隔二上生之理)七弦羽益之亦生五弦角(此亦隔
一下生 )
此三弦宫声损而上生得第三弦至第七弦若三弦
卷上 第 11b 页 WYG0220-0700d.png
宫声上下相生损益并用得第一弦至第七弦之七弦
矣此五音相生得七弦之次第以合弦之巨细者也凡
此乃七弦得五声自然之至理而不可易者若以一弦
为宫岂能穷律吕贯通之妙哉白虎通曰八音法易八
卦丝离音也盛德在火其音徵一弦尚徵不益信哉兹
特绘三图于左使纲举而目张庶一弦尚徵之义显然
无遁情矣
卷上 第 12a 页 WYG0220-0701a.png
按三分损益相生之法三弦宫为八十一益而下生一
卷上 第 12b 页 WYG0220-0701b.png
弦倍徵之一百有八一弦倍徵损而上生四弦商之七
十二四弦商益而下生二弦倍羽之九十六二弦倍羽
损而上生五弦角之六十四得倍徵第一弦至角声第
五弦
卷上 第 13a 页 WYG0220-0701c.png
三弦宫损而上生六弦徵之五十四六弦徵益而下生
卷上 第 13b 页 WYG0220-0701d.png
四弦商之七十二四弦商损而上生七弦羽之四十八
七弦羽益而下生五弦角之六十四得宫声第三弦至
羽声第七弦
卷上 第 14a 页 WYG0220-0702a.png
三弦宫声损益并用上下相生得倍徵第一弦至羽声
卷上 第 14b 页 WYG0220-0702b.png
第七弦○琴止用五正声五音相生始于宫终于角故
三弦宫声上下相生皆至五弦角声而止三弦之左无
连线即始于宫无声以生宫也五弦之右无连线即终
于角角声无声以生也
三准当徽不当徽之别
琴徽之定位以岳山至焦尾全度之中为七徽七徽上
至岳山之度半之为四徽四徽又上至岳山之度半之
卷上 第 15a 页 WYG0220-0702c.png
为一徽七徽下至焦尾之尾半之为十徽十徽又下至
焦尾之度半之为十三徽又以岳山至焦尾全度三分
之一分为五徽二分为九徽五徽上至岳山之度半之
为二徽九徽下至焦尾之度半之为十二徽又以岳山
至焦尾全度五分之一分为三徽二分为六徽三分为
八徽四分为十一徽此琴十三徽折取之定位也取音
亦有不在徽之位者以五音相生之度有当徽不当徽
之别也惟七徽四徽一徽俱当徽而七弦皆用得本弦
之正声又谓之三准(七徽为全度之半七徽至焦尾为下准四徽为七
卷上 第 15b 页 WYG0220-0702d.png
徽之半四徽至七 )
卷上 第 16a 页 WYG0220-0703a.png
(徽为中准一徽为四徽之半一徽至四徽为上准)(十三徽十二徽十
一徽八徽)
六徽三徽俱不当取音之正位十徽九徽五徽二徽取
音虽亦当徽而七弦之中间有不用者要皆以徽分与
五声二变之度并举而详覈之其理始明焉以下准言
之十三徽一弦用之为九十六之倍羽位三弦用之为
七十二之商位四弦用之为六十四之角位六弦用之
为四十八之羽位此十三徽二弦五弦七弦不用而一
卷上 第 16b 页 WYG0220-0703b.png
弦三弦四弦六弦俱用焉五声之度俱在十三徽下一
分故十三徽不当取音之正位十二徽
二弦用之为八十一之宫位五弦用之为五十四之徵
位七弦用之为四十零五之少宫位此十二徽一弦三
弦四弦六弦不用而二弦五弦七弦俱用焉五声之度
俱在十二徽下二分故十二徽亦不当取音之正位十
一徽惟三弦用之为六十四之角位馀弦俱不用独三
弦用之五声之度在十一徽上二分故十一徽亦不当
取音之正位十徽一弦用之为八十一之宫位二弦用
卷上 第 17a 页 WYG0220-0703c.png
之为七十二之商位四弦用之为五十四之徵位五弦
用之为四十八之羽位六弦用之为四十零五之少宫
位七弦用之为三十六之少商位此十徽独三弦不用
馀弦皆用之焉九徽一弦用之为七十二之商位二弦
用之为六十四之角位三弦用之为五十四之徵位四
弦用之为四十八之羽位六弦用之为三十六之少商
位七弦用之为三十二之少角位此九徽独五弦不用
卷上 第 17b 页 WYG0220-0703d.png
馀弦皆用之焉八徽一弦用之为六十四之角位三弦
用之为四十八之羽位六弦用之为三十二之少角位
此八徽二弦四弦五弦七弦不用而一弦三弦六弦俱
用焉五声之度俱在八徽上一分故八徽亦不当取音
之正位七徽为全度之半各弦用之为本弦正声五弦
四十零五之少宫位在八徽半二弦五十四之徵位四
弦四十零五之少宫位五弦三十六之少商位七弦二
十七之少徵位俱在七徽六分此数声者盖又居无徽
之分焉至于各弦二变之声一弦八十五三二之变宫
卷上 第 18a 页 WYG0220-0704a.png
位在十徽二分五十六八八之变徵位在
七徽三分二弦八十五三三之变宫位在十三徽一分
五十六八八之变徵位在七徽九分三弦五
十六八八之变徵位在九徽四分四十二六六之少变
宫位在七徽三分四弦五十六八八之变徵位在十徽
八分四十二六六之少变宫位在七徽九分五弦五十
六八八之变徵位在十三徽一分四十二六六之少变
卷上 第 18b 页 WYG0220-0704b.png
口位在九徽六弦四十二六六之少变宫位在十徽八
分二十八四四之少变徵位在七徽三分七弦四十二
六六之少变宫位在十三徽一分二十八四四之少变
徵位在七徽九分此下准焦尾至七徽各弦五声二变
之度分也以中准言之六徽乃十一徽之半各弦用之
与十一徽同五徽乃九徽之半各弦用之与九徽同四
徽乃七徽之半各弦用之与七徽同七徽至四徽谓之
中准各徽得下准各徽之半而同声无徽之分惟五徽
七分得下准十徽之半而同声其馀俱得下准无徽之
卷上 第 19a 页 WYG0220-0704c.png
分之半而同声焉六徽四分与十三徽一分同六徽二
分与十二徽二分同五徽九分与十徽八分同五徽二
分与九徽四分同四徽八分与八徽半同四徽六分与
七徽九分同四徽四分与七徽六分同四徽二分与七
徽三分同此中准七徽至四徽各弦五声二变之度分
也以上准言之三徽乃六徽之半各弦用之同于十一
徽六徽矣二徽乃五徽之半各弦用之同于九徽五徽
卷上 第 19b 页 WYG0220-0704d.png
矣一徽乃四徽之半各弦用之同于七徽四徽矣四徽
至一徽谓之上准各徽亦得中准各徽之半而同声至
于无徽之分三徽四分则同于十三徽一分与六徽四
分三徽二分则同于十二徽二分与六徽二分二徽九
分则同于十徽八分与五徽九分二徽七分则同于十
徽与五徽七分二徽二分则同于九徽四分与五徽二
分一徽八分则同于八徽半与四徽八分一徽六分则
同于七徽九分与四徽六分一徽四分则同于七徽六
分与四徽四分一徽二分则同于七徽三分与四徽二
卷上 第 20a 页 WYG0220-0705a.png
分此上准四徽至一徽各弦五声二变之度分也一徽
之上不能为用矣今以各弦全度五声多寡之分与三
准各徽分所得五声二变之位列图为表审音者亦将
有所取衷焉
卷上 第 20b 页 WYG0220-0705b.png
凡弦之巨者分数多弦之细者分数少如倍徵一百八
纶则定为一百八分倍羽九十六纶则定为九十六分
宫弦八十一纶则定为八十一分馀仿此各弦得声之
位其长短参差不同有此徽同者在彼徽则异有彼分
同者至此分又异何也因羽与宫角与徵相去之度长
而变宫变徵之不为用者间于其中也按五声二变之
位惟二变无散声相应五声之位按巨弦则细弦之散
声应按细弦则巨弦之散声应两弦俱按则五声二变
之数相同亦莫不相应也而此中则有中准上准音节
卷上 第 21a 页 WYG0220-0705c.png
之半数与半而又半之数即如一弦四徽之二十七分
一徽之十三分小馀五皆为徵声二弦四徽之二十四
分一徽之十二分皆为羽声是也馀仿此恐阅者以数
之互异不能辨识故绘弦音倍半之图于后以示之
卷上 第 21b 页 WYG0220-0705d.png
卷上 第 22a 页 WYG0220-0706a.png
泛音四准
泛音不假按抑得自然之声虽与实音稍异要不外乎
五声二变之理盖实音有三准每准之内不拘某弦俱
得五声二变之七声不论当徽不当徽但遇五声二变
度分俱可按其度分而得声也至于泛音则当为四准
每四准之内一弦四弦六弦得二正声一变声二弦七
弦得二正声三弦得三正声五弦得一正声一变声必
于徽间始有声否则无声盖一徽四徽七徽十徽十三徽
卷上 第 22b 页 WYG0220-0706b.png
声相同二徽五徽九徽十二徽声相同三徽六徽八徽
十一徽声相同故有三声其有祇得二声者徽不遇五
声二变之度分故也以各徽所得之五声二变言之一
徽四徽七徽十徽十三徽俱得本弦之正声
(四徽七徽十徽十三徽皆属徵二弦属羽则一徽四徽七徽十徽十三
䘗皆属羽是也馀仿此 二徽五)
徽九徽十二徽俱得本弦正声相生之声
(得商声二弦七弦属羽羽生角得角声三弦属宫宫生徵得徵声四弦
属商商生羽得羽声五弦属角角生变 )
三徽六徽八徽十一徽在三弦则得角声角生
变宫故在一弦六弦而得变宫之声变宫生变徵故在
卷上 第 23a 页 WYG0220-0706c.png
四弦而得变徵之声变徵生清宫故在二弦七弦而得
清宫之声有其位而不用清宫生清徵故在五弦而得
清徵之声有其位而不用(此隔一下生隔二上生之理也三弦之三徽
六徽八徽十 )
(一徽之角声生一弦六弦三徽六徽八徽十一徽之变宫声即如三弦
宫声与三弦一徽四徽七徽十徽十三 )
(徽宫生一弦六弦徵声与一弦六弦一徽四徽七徽十一徽十三徽徵
声之比三弦二徽五徽九徽十二徽徵 )
(声生一弦六弦二徽五徽九徽十二徽商声之比也)(此各弦泛音得
各徽五声二)
变之大槩也以各徽相对而音相同者言之六徽与八
卷上 第 23b 页 WYG0220-0706d.png
徽相对五徽与九徽相对四徽与十徽相对三徽与十
一徽相对二徽与十二徽相对一徽与十三徽相对徽
相对而所出之音必相同者无他由焦尾至七徽中间
各徽之五声二变度分与岳山至七徽中间各徽之五
声二变度分彼此相同故也大抵泛音之取音以七徽
居中为界划七徽上至岳山下至焦尾分而为二实音
附木取音不论徽之远近俱自岳山一边而出泛音以
指浮弦上徽之上下皆为震动则徽之上下皆有声出
去岳山远则声低而浊近则声高而清高而清之声既
卷上 第 24a 页 WYG0220-0707a.png
出低而浊之声自不能出矣如六徽至一徽在七徽之
上得声之清所出五声二变度分之声与实音相同八
徽至十三徽在七徽之下得声之浊合诸五声二变度
分不能出声所出之声乃从焦尾至各徽而出故不得
与实音相同也即就一弦所值之徽而论一弦七徽居
全度之中上至岳山下至焦尾远近相均同为五十四
之徵其声清浊互出得本弦之正声六徽为四十二六
卷上 第 24b 页 WYG0220-0707b.png
六之变宫位(皆五声二变之半或半之又半俱不细注)(五徽为三十
六之商)
位四徽乃七徽之半为二十七之本弦徵位三徽乃六
徽之半为二十一三三之变宫位二徽乃五徽之半为
十八之商位一徽乃四徽之半为十三五之本弦徵位
此七徽之上六徽俱得本弦五声二变度分由声之清
故得与实音相同八徽为六十四之角位泛音乃变宫
声盖自焦尾计至八徽乃四十二六六之变宫位也九
徽为七十二之商位泛音亦得商声此九徽适合者自
焦尾计至九徽乃三十六之商位合实音七十二商声
卷上 第 25a 页 WYG0220-0707c.png
之半倍半之声原相同也十徽为八十一之宫位泛音
乃徵声自焦尾计至十徽乃七徽之半为二十七之本
弦徵位也十一徽为八十五三三之变宫位泛音亦得
变宫声此十一徽适合者自焦尾计至十一徽乃八徽
之半为二十一三三之变宫位合实音八十五三三变
宫半之又半倍半而又半声亦相同也十二徽一弦原
无五声二变之位泛音得声为商声自焦尾计至十二
卷上 第 25b 页 WYG0220-0707d.png
徽乃九徽之半为十八之商位也十三徽为九十六之
羽位泛音乃徵声自焦尾计至十三徽乃十徽之半为
十三五之本弦徵位也此七徽之下六徽由声之浊不
与实音相同俱得焦尾至七徽五声二变度分之清声
焉(馀弦俱未细注阅后之绘图自明)(故七徽上下必判而为二七徽
之)
上四徽至七徽为上之下准一徽至四徽为上之上准
七徽之下十徽至七徽为下之上准十三徽至十徽为
下之下准此泛音之四准与实音之得声自有分别也
今特详列其图于左
卷上 第 26a 页 WYG0220-0708a.png
卷上 第 26b 页 WYG0220-0708b.png
七徽以上各弦七下所载五声之数皆相同由岳山起
至焦尾得声之清泛音实音声相同也七徽以下各弦
上所载五声之数为泛音自焦尾起至岳山亦得声之
清各弦下所载五声之数为实音自岳山起至焦尾得
声之浊审音者试以散声和之则七徽以上之泛音由
岳山至七徽度短七徽以下之泛音由焦尾至七徽度
亦短俱得声之清而清声为用浊声不能为用之理自
明矣
卷上 第 27a 页 WYG0220-0708c.png
按声散声相和说
鼓宫宫应弹角角动音相准也故徽分之位恒与散声
相和向来注谱之家类多错认分数斯律之能协者寡
矣兹特以弦度五声之数较定徽分于后而两言以该
之曰按弹外散扣内按弹内散扣外试以按弹外散扣
内言之间四弦者按七徽间三弦者二弦则按七徽六
分一弦三弦则按七徽九分间两弦者按九徽间一弦
者各弦俱按十徽惟三弦按十徽八分两弦相连者二
卷上 第 27b 页 WYG0220-0708d.png
弦五弦则按十二徽二分一弦三弦四弦六弦则按十
三徽一分此皆按弹外散扣内也皆正声之相和者也
以按弹内散扣外言之间四弦者亦按七徽两弦相连
者二弦四弦五弦七弦则按七徽六分三弦六弦则按
七徽九分间一弦者惟五徽按八徽半馀弦俱按九徽
间两弦者按十徽间三弦者五弦七弦则按十二徽二
分六弦则按十三徽一分此皆按弹内散扣外也皆倍
声之相和者也至七徽为正声之半和以正声之倍亦
按弹内散扣外此则倍声之倍之相和者也其有不相
卷上 第 28a 页 WYG0220-0709a.png
和而实可和者乃相生之声相和亦必按弹内散扣外
(如按弹外散扣内虽亦得相生之位而声音乖舛不可为用)(间两弦
者按七徽 如按 弹七 )
(弦羽声应散扣四弦商声商生羽而相和也按弹六弦徵声应散扣三
弦宫声宫生徵而相和也馀可类推 )
(此俱散声生按声也若按声生散声音虽不乖舛谱亦不多用)(间三
弦者五弦七弦则)
按七徽六分六弦则按七徽九分间四弦者按九徽两
弦相连者二弦四弦五弦七弦则按十徽三弦六弦则
按十徽八分盖三弦十徽八分之位为角应二弦羽自
卷上 第 28b 页 WYG0220-0709b.png
当按十徽八分至于六弦原不当按十徽八分之位所
以按之者因六弦十徽之位为宫不与五弦角相和惟
十徽八分为变宫之位与五弦角声相生而相和故按
之耳间一弦者惟五弦按十二徽二分馀弦俱按十三
徽一分夫七弦之十二徽二分亦为宫位而按十三徽
一分者十三徽一分亦变宫之位应五弦角声也故同
一按弹内散扣外而此之相和有不可以倍声例者盖
相生之声之相和者也以上乃下准之各徽分得各弦
散声相和之大要若中准上准之徽分与下准之徽分
卷上 第 29a 页 WYG0220-0709c.png
同亦得各弦散声相和之声焉(如按一弦中准五徽之三十六分上准
二徽之 )
(十八分六弦中准五徽之十八分上准二徽之九分俱应四弦散声之
七十二分盖弦音之半半而又半半之 )
然亦有两弦俱散扣而相和者间四弦者
本弦之声得倍半而相和一弦为六弦之倍二弦为七
弦之倍是也间两弦者乃相生之声相和如一弦徵生
四弦商二弦羽生五弦角是也间一弦者惟五弦角不
与三弦宫相和馀亦以相生之声相和如三弦宫生一
卷上 第 29b 页 WYG0220-0709d.png
弦徵四弦商生二弦羽是也总而言之各弦相应之声
不出乎正声倍声与相生之声三者之范围故并著其
同异以明之(同者谓倍声与正声相同异者谓相生之声与正声较其
数实异也 )
三弦独下一徽
宋姜夔七弦琴图说曰七弦散而扣之则间一弦于第
十徽取应声如宫调五弦十徽应七弦散声四弦十徽
应六弦散声二弦十徽应四弦散声大弦十徽应三弦
散声惟三弦独退一徽于十一徽应五弦散声古今无
知之者窃谓黄钟大吕并用慢角调故于大弦十一徽
卷上 第 30a 页 WYG0220-0710a.png
应三弦散声太蔟夹钟并用清商调故于二弦十一徽
应四弦散声姑洗仲吕蕤宾并用宫调故于三弦十一
徽应五弦散声林钟夷则并用慢宫调故于四弦十一
徽应六弦散声南吕无射应钟并用蕤宾调故于五弦
十一徽应七弦散声以律长短配弦大小各有其序
愚谓斯言祗得乎五调下一徽之当然而未明乎
宫调三弦独下一徽之所以然何也彼泥于律吕长短
卷上 第 30b 页 WYG0220-0710b.png
之说而未以弦度之五声数详覈之也按管子曰凡将
起五音凡首先主一而三之四开以合九九以是生黄
钟小素之首以成宫三之三因也四开四分也
九九八十一也黄钟宫声也素煮沤白练乃熟丝即弦
也小素即小弦也谓将起五音以倍徵一弦之全度三
因之得三倍复四分为八十一宫位之度其弦之小于
一弦者与此度之声相应得宫声因宫为声之始而以
此度为起音之首耳以五声数细较之则按一弦之十
徽而应乎三弦之散声(如琴之全度三尺六寸自岳山至四徽为九寸
卷上 第 31a 页 WYG0220-0710c.png
至七徽为一尺 )
卷上 第 31b 页 WYG0220-0710d.png
(八寸至十徽为二尺七寸至焦尾为三尺六寸以三尺六寸而三因之
则为一丈零八寸以一丈零八寸而四 )
(分之则为二尺七寸适在十徽之位与一弦之一百有八三因而四分
之得八十一之数正相合也十徽系常 )
(用之位得本弦相和之音与本弦与九徽相和之音同因九徽隔二和
以散声之正隔一和以散声之倍十徽 )
(则隔一和以散声之正隔二和以散声之倍故也审音者知九徽乃本
弦相生得我生之声而相和若于十徽 )
(自全度损益相生皆不能及其位予细审所以与本弦相和者乃生本
弦之声故尔也十徽为全度四分之三 )
(三分益一分则为四分是十徽之位生全度散声得生我之声故亦相
和也管子用三其实而四其法以覈之 )
(自得生我之声即司马氏律书四其实或倍其实而三其法以得我生
之声之理也古人审音之蜜取法之简 )
卷上 第 32a 页 WYG0220-0711a.png
盖倍徵之一弦其全度计一百有八分三因之
则为三百二十四以三百二十四而四分之则为八十
一一弦十徽即宫声八十一之分而三弦全度亦宫声
八十一之分故一弦十徽应三弦散声也夫一弦属徵
既得生徵之宫于十徽以应乎三弦之散声则馀弦自
当以五声数用三因四分之法较之而三弦独下一徽
之理自明矣故以倍羽二弦全度九十六分而三因之
则为二百八十八以二百八十八而四分之则为七十
二矣二弦十徽即商声七十二之分而四弦全度亦商
卷上 第 32b 页 WYG0220-0711b.png
声七十二之分故二弦十徽应四弦散声也以商声四
弦全度七十二分而三因之则为二百一十六以二百
一十六而四分之则为五十四矣四弦十徽即徵声五
十四之分而六弦全度亦徵声五十四之分故四弦十
徽应六弦散声也以角声五弦全度六十四分而三因
之则为一百九十二以一百九十二而四分之则为四
十八矣五弦十徽即羽声四十八之分而七弦全度亦
卷上 第 33a 页 WYG0220-0711c.png
羽声四十八之分故五弦十徽应七弦散声也以上各
弦俱按十徽而与散声应惟三弦则独按十一徽以应
五弦之散声者非有他也亦就三弦之分数与五弦之
全度相较而得之耳盖宫声三弦之全度本八十一分
三因之则为二百四十三以二百四十三而四分之则
为六十零七五夫三弦之十徽固六十零七五之分矣
(按六十零七五之数比变徵五十六八八则有馀比角六十四则不足
比清角五十九九二虽不及一分然声 )
(音之辨毫釐不紊又不得谓之清角盖十徽为生散声之位如一弦徵
十徽宫所生也二弦羽十徽商所生也 )
(四弦商十徽徵所生也五弦角十徽羽所生也三弦为宫无生宫之声
卷上 第 33b 页 WYG0220-0711d.png
故三弦十徽六十零七五之分非按声 )
卷上 第 34a 页 WYG0220-0712a.png
而五弦之全度则为角声六十四之分必按乎三弦
角声六十四之分始克应乎五弦之全度也而三弦角
声六十四之分实在十一徽此三弦之所以独下一徽
以应五弦之散声者也
五弦独上半徽
五弦独上半徽古今未有论及者大抵调琴必于十徽
九徽审音之高下为定弦之规如散扣七弦有间一弦
卷上 第 34b 页 WYG0220-0712b.png
而于五弦按十徽以取应声者有间二弦而于四弦按
九徽以取应声者一散一按次第定弦以至于一弦而
弦胥定矣三弦之按十一徽常及用也五弦之按八徽
半不及用也盖散扣内之细弦按弹外之巨弦五声之
数固相和(三弦为八十一之分一弦十徽亦八十一之分四弦为七十
二之分一弦九徽亦七十二 )
而按弹内之细弦散扣外之巨弦细弦按声适合巨
弦散声五声之倍数亦相和也(七弦十徽为三十六之分乃商声之半
应四弦 )
(七十二商声之正七弦九徽为三十二之分乃角声之半应五弦六十
四角声之正丝乐倍半声相和倍律对 )
(正律言为倍正律对半律言亦为倍也)(试言之七弦十徽应四弦散
卷上 第 35a 页 WYG0220-0712c.png
声六)
卷上 第 35b 页 WYG0220-0712d.png
弦十徽应三弦散声五弦十徽应二弦散声四弦十徽
应一弦散声此十徽按弦应散声之倍数也
七弦九徽应五弦散声六弦九徽应四弦散声四
弦九徽应二弦散声三弦九徽应一弦散声此九徽按
弦应散声之倍数也惟五弦独上半徽以应三弦之散
声何也三弦和五弦散声必下一徽则五弦和三弦散
声亦必上半徽也(十徽至十一徽度短九徽至八徽度长上半徽之度
与下一徽之度长短 )
卷上 第 36a 页 WYG0220-0713a.png
夫十徽之分为全度四分之三以全度散声为四分
三分而益一分为四分则十徽之分生全度散声
(一分则为二分则十徽之分又生七徽之分矣七徽乃全度之半其理
同也 独三弦之十徽)
无按声之位者即五音相生始于宫之理宫为君声不
能有生宫之声三弦为宫故三弦之十徽无按声之位
必下一徽始应五弦散声既用管子审音之法覈之矣
若九徽之分为全度三分之二以全度散声为三分三
分而去一分为二分则全度散声生九徽之分独五弦
之九徽无按声之位者即五音相生终于角之理琴止
卷上 第 36b 页 WYG0220-0713b.png
用五正声角生变声而不能生正声五弦为角故五弦
之九徽无按声之位必上半徽始应三弦散声是当用
五音相生之法覈之也何也九徽之五声皆本弦相生
之声九徽为全度三分去一之位则各弦之声不皆三
分去一而得相生之声哉即如七弦羽声羽生角也九
徽乃三十二角声之半故应五弦角散声六弦徵声徵
生商也九徽乃三十六商声之半故应四弦商散声四
卷上 第 37a 页 WYG0220-0713c.png
弦商声商生羽也九徽乃四十八之羽位故应二弦倍
羽散声三弦宫声宫生徵也九徽乃五十四之徵位故
应一弦倍徵散声至于五弦角声角生变宫九徽乃四
十二六六系变宫之半变宫本无散声以相和也
(五声之正二变虽有其位不用)(须知五弦既应以三弦而三弦固宫
声)
也宫必以宫相应而惟五弦四十零五宫声之半位实
在八徽半此五弦之所以独上半徽以应三弦宫之散
声也
卷上 第 37b 页 WYG0220-0713d.png
律吕名徽辨
琴徽之义自来未有考据予观近代琴谱以十二律吕
名十二徽曰十二徽象十二月中之第七徽象闰于是
定第一徽为正月起太蔟第十二徽为十一月起黄钟
转相师授牢不可破而不知其非也十三徽之位之疏
密与十二律吕之度之长短细细较对迥不相侔使比
而同之声音失其序矣且弦有巨细即音皆有异徽分
系各弦取音之节即应得用之声字皆随弦而递迁使
卷上 第 38a 页 WYG0220-0714a.png
定一弦之第一徽为太蔟第十二徽为黄钟则二三四
五弦之第一徽俱不得为太蔟其第十二徽俱不得
黄钟矣彼以律吕名徽者岂其未见及此耶夫琴有十
三徽止用五声二变之七音故每弦之取音于徽者一
徽二徽四徽五徽七徽九徽十徽而已其馀皆不得取
音之位也而一徽四徽七徽音又相同二徽五徽九徽
音又相同则亦止得三声其更有止得二声者三弦是
也十徽无按声亦不得取音之位也夫七音之取于十
三徽者尚止得三声二声而顾以十二律吕配夫十二
卷上 第 38b 页 WYG0220-0714b.png
徽而欲得十二声也能乎古人立法原自简易以弦音
之倍半声相同于是二分之而定以七徽四徽一徽焉
盖七徽为全度之半四徽为七徽之半一徽又为四徽
之半皆本弦之正声故也以声之相和为用乃相生之
声于是三分之而定以九徽五徽二徽焉盖九徽为全
度三分之二五徽为九徽之半二徽又为五徽之半皆
本弦相生之声故也至于十徽乃自七徽至焦尾之半
卷上 第 39a 页 WYG0220-0714c.png
位也泛音得七徽之半声而声相同(泛音相同之理详见泛音四准篇
)
按声与七徽之声则不相同而相和盖十徽为全度四
分之三乃本弦生声之始故亦得声之相和也
(分之三七徽乃全度四分之二十徽之声为三分损一分则生七徽之
声益一分则生全度之散声故为本弦 )
(生声之始生我之声与我生之声相和之理同也)(统计十徽九徽七
徽五徽四)
徽二徽一徽之位得本弦弦音倍半与三分损益相生
之理而定故本弦之声生我之声与我生之声皆得以
取音于徽焉(如一弦徽声则七徽属徵为本弦之声十徽属宫宫生徵
为我生之声九徽属商徽生 )
(商为我生之声馀弦皆可类推)(惟十三徽十二徽及十一徽八徽六
卷上 第 39b 页 WYG0220-0714d.png
徽)
卷上 第 40a 页 WYG0220-0715a.png
三徽则皆不得乎取音之位十三徽十二徽不得取音
之位者以自焦尾至十徽九徽得倍半声乃为泛音自
然之声而定按声则非本弦倍半声亦非本弦相生之
声故尔也以十三徽言之十三徽乃十徽至焦尾之半
位其泛音自与七徽十徽之泛音同若于此作按声其
音必不合必下一分当九徽上三分益一之位而始合
盖十三徽因七徽为泛音折半取音而定上至岳山折
卷上 第 40b 页 WYG0220-0715b.png
半而得四徽再折半而得一徽下至焦尾折半而得十
徽再折半而得十三徽故在泛音为得弦音倍半之理
而与七徽十徽同按声则因九徽相生而来故不与七
徽十徽同而不得取音之位也以十二徽言之十二徽
乃九徽至焦尾之半位其泛音自与九徽之泛音同若
于此作按声其音亦不合必下二分当八徽半上三分
益一之位而始合盖十二徽因九徽为泛音亦折半取
音而定上至岳山折半而得五徽再折半而得二徽下
至焦尾折半而得十二徽故在泛音亦得弦音倍半之
卷上 第 41a 页 WYG0220-0715c.png
理而与九徽同按声则因八徽半相生而来故不与九
徽同而亦不得取音之位也十一徽八徽六徽三徽亦
不得取音之位者以全度五分亦为泛音自然之声而
定十一徽之按声在七徽九分上三分益一之位若按
十一徽其音亦不合必上二分而始合六徽实为十一
徽之半三徽又为六徽之半其声同矣声相同而按之
其不合也犹之十一徽也八徽之按声在十三徽一分
卷上 第 41b 页 WYG0220-0715d.png
上三分损一之位若按八徽其音亦不合必上一分而
始合盖全度五分取分相均皆为泛音而定故泛音皆
相同论其按声则十一徽六徽三徽因七徽九分相生
而来故与八徽之按声不同八徽因十三徽一分相生
而来故与十一徽六徽三徽之按声不同俱不得取音
之位也盖五声二变之位定于三分损益之长短若十
三徽之位则因泛音自然之声而定止于二分之三分
之五分之之三者故止得三音岂能合乎五声二变之
七音哉兹即下准之弦度得五声二变之位于徽分而
卷上 第 42a 页 WYG0220-0716a.png
以三分损益之法覈之十徽固本弦生声之始也管子
有曰将起五音凡首先主一而三之四开以合九九以
生黄钟小素之首以成宫此非指倍徵一弦之十徽宫
位为起音之本乎十徽之位三分之而益一分则为全
度之散声(损一分则生七徽之声与生散声之理同其十徽为三分则
全度为四分七徽为二分四 )
(徽为一分四分二分一分声相同盖一分为二分之半二分又为四分
之半此弦音倍半声相同之理故三分 )
(之位而损益之损一分生二分之声益一分生四分之声也馀仿此又
不拘某徽分指为四分三分二分一分 )
卷上 第 42b 页 WYG0220-0716b.png
(者自此度至彼度长短相均如十徽为三分就一弦之一百有八分而
论则岳山至四徽得二十七分四徽至 )
(七徽亦得二十七分七徽至十徽亦得二十七分十徽至焦尾亦得二
十七分如全度为三分亦就一弦而论 )
(岳山至五徽得三十六分五徽至九徽亦得三十六分九徽至焦尾亦
得三十六分馀仿此而损益相生之理 )
于是一弦十徽宫位生一弦徵散声二弦十徽商
位生二弦羽散声若三弦乃宫声五弦相生始于宫终
于角无生宫之声所以宫为声之始而三弦之十徽无
有按声之位也四弦十徽徵位生四弦商散声五弦十
徽羽位生五弦角散声(六弦七弦为一弦二弦之半得声之理与一弦
二弦同俱不录 )
此各弦十徽之声生各弦之散声者也又以全度之散
卷上 第 43a 页 WYG0220-0716c.png
声三分之而损一分其位则在九徽(全度为三分九徽为二分五徽为
一 )
于是一弦徵散声生九徽商位二弦羽散声生九徽
角位三弦宫散声生九徽徵位四弦商散声生九徽羽
位五弦角散声生九徽变宫位夫五弦角独生变声者
即五音相生始于宫终于角之理自宫徵商羽次第相
生至角而止皆正声惟角不能生正声而生变声所以
角为声之终也论五弦之宫位实在八徽半似当自六
卷上 第 43b 页 WYG0220-0716d.png
徽七分相生而五弦之六徽七分无按声之位
故五弦角必生九徽变宫也此各弦散声生
九徽之声者也又以九徽之位三分之而益一分其位
则在十三徽一分(九徽为三分十三徽一分为四分六徽四分为二分
三徽四分为一分 )
更以八徽半之位三分之而益一分其位则在十二徽
二分(八徽半为三分十二徽二分为四分六徽二分为二分三徽二分
为一分 于是一弦九)
徽商位生十三徽一分羽位二弦九徽角位生十三徽
一分变宫位论二弦之宫位在十二徽二分当自八徽
半相生而二弦之八徽半无按声之位故九徽角生十
卷上 第 44a 页 WYG0220-0717a.png
三徽一分变宫也三弦九徽徵位生十三徽一分商位
四弦九徽羽位生十三徽一分角位五弦九徽变宫位
生十三徽一分变徵位其八徽半宫位生十二徽二分
徵位此九徽与八徽半之声生十三徽一分与十二徽
二分之声者也又以十三徽一分之位三分之而损一
分其位则在七徽九分(十三徽一分为三分七徽九分为二分四徽六
分为一分 以)
十二徽二分之位三分之而损一分其位则在七徽六
卷上 第 44b 页 WYG0220-0717b.png
分(十二徽二分为三分七徽六分为二分四徽四分为一分)(于是一
弦十三徽一分)
羽位生七徽九分角位二弦十三徽一分变宫位生七
徽九分变徵位其十二徽二分宫位生七徽六分徵位
三弦十三徽一分商位生七徽九分羽位四弦十三徽
一分角位生七徽九分变宫位论四弦之宫位在七徽
六分当自十二徽二分相生而四弦之十二徽二分无
按声之位故十三徽一分角生七徽九分变宫也五弦
十三徽一分变徵位生七徽九分清宫而不用夫始于
宫终于角者以五音相生皆正声至角止而生变声也
卷上 第 45a 页 WYG0220-0717c.png
琴既用二变因终于变徵故变徵所生之位不得为用
其十二徽二分徵位生七徽六分商位此十三徽一分
与十二徽二分之声生七徽九分与七徽六分之声者
也又以七徽九分之位三分之而益一分其位则在十
徽八分(七徽九分为三分十徽八分为四分五徽九分为二分二徽九
分为一分 以七徽六)
分之位三分之而益一分其位则在十徽
(四分五徽七分为二分二徽七分为一分)(于是一弦七徽九分角位
生十徽)
卷上 第 45b 页 WYG0220-0717d.png
八分变宫位论一弦之宫位在十徽当自七徽六分相
生而一弦之七徽六分无按声之位故七徽九分角生
十徽八分变宫也管子所谓一弦十徽为起音之本者
此也二弦七徽九分变徵位生十徽八分清宫而不用
其七徽六分徵位生十徽商位三弦七徽九分羽位生
十徽八分角位四弦七徽九分变宫位生十徽八分变
徵位其七徽六分宫位生十徽徵位五弦七徽六分商位
生十徽羽位此七徽九分与七徽六分之声生十徽八
分与十徽之声者也又以十徽八分之位三分之而损
卷上 第 46a 页 WYG0220-0718a.png
一分其位则在七徽三分(十徽八分为三分七徽三分为二分四徽二
分为一分 )
以十徽之位三分之而损一分其位则在七徽
于是一弦十徽八分变宫位生七徽三分
变徵位三弦十徽八分角位生七徽三分变宫位四弦
十徽八分变徵位生七徽三分清宫而不用若十徽之
声所生七徽之声原与生散声者相同不再赘此固十
徽八分之声生七徽三分之声者也又以七徽三分之
卷上 第 46b 页 WYG0220-0718b.png
位三分之而益一分其位则在九徽四分
(分为四分五徽二分为二分二徽二分为一分)(以七徽之位三分之
而益一分)
其位则在九徽
于是一弦七
徽三分变徵位生九徽四分清宫而不用三弦七徽三
分变宫位生九徽四分变徵位若七徽之声所生九徽
之声原与散声生九徽之声相同亦不赘此固七徽三
分之声生九徽四分之声者也又以九徽四分之位三
分之而损一分其位则在六徽七分(九徽四分为三分六徽七分为二
卷上 第 47a 页 WYG0220-0718c.png
分 )
卷上 第 47b 页 WYG0220-0718d.png
于是三弦九徽四分变徵位生六徽七分清
宫而不用此九徽四分之声生六徽七分之声者也至
于六徽七分之位则皆清声而无所用故不载总之下
准各弦之度以损益相生得五声二变之位惟十徽九
徽七徽得其声其馀诸徽与三弦之十徽俱不能得其
声焉(各弦五声二变之位所为宫声为始角声生变宫而终于变徽者
其理丝毫不紊 各弦分七音之 )
(位实有旋转不息之义自十徽生散声与七徽散声与七徽生九徽九
徽生十三徽一分十三徽一分生七徽 )
(九分七徽九分生十徽八分十徽八分生七徽三分七徽三分生九徽
四分九徽四分生六徽七分以六徽七 )
卷上 第 48a 页 WYG0220-0719a.png
(分之位三分之而益一分其位在八徽半则六徽七分实生八徽半八
徽半生十二徽二分十二徽二分生七 )
(徽六分七徽六分生十徽而仍归原位未尝不与十二律吕隔八相生
之理有合也 至若中准为)
下准之半上准又为中准之半三分损益之理固一致
也特以三准五声二变之位计之实得三十有六使依
此得声之位以定徽则其中有长有短有疏有密矣下
准之度音节长遇其密者犹可定中准上准之度音节
短遇其密者则太密而难分辨其序故不若二分之三
分之五分之以泛音自然之位而定以十三徽之为妙
耳曾何十二律吕配十三徽而月而闰之扰扰乎夫五
卷上 第 48b 页 WYG0220-0719b.png
声二变之于十三徽止得三声二声岂十二律吕配夫
十三徽而反能得夫十二声也乎古之以律吕配月者
相生损益自然之序也必谓十二月象徽数而以十二
律吕强名之噫嘻亦不经甚矣余故详辨之更以二分
之得七徽四徽一徽十徽十三徽者为一图以三分之
得九徽五徽二徽十二徽者为一图以五分之得八徽
十一徽六徽三徽者为一图序列于后俾人知徽所由
卷上 第 49a 页 WYG0220-0719c.png
定祇因自然之泛音而不得强作解事藉口于律吕庶
古圣人作乐之遗意犹可遇诸丝桐间也
卷上 第 49b 页 WYG0220-0719d.png
卷上 第 50a 页 WYG0220-0720a.png
释黄钟均以仲吕为角之疑
朱子琴律曰古之为乐者通用三分损益隔八相生之
法若以黄钟为宫则姑洗之为角有不可以毫发差者
而今世琴家独以仲吕为黄钟之角故于众乐常高一
律惟第三弦本是角声乃得守其旧而不变流传既久
虽不知其所自来然听以心耳亦知非人力所能为也
昔人亦有为之说者皆无足取其曰五声之象角实为
以民为贵故于此焉上之者则穿凿而迂疏亦已甚矣
近世惟长乐王氏之书所言礼乐最为近古然其说琴
卷上 第 50b 页 WYG0220-0720b.png
亦但以第三弦为律中仲吕而不言其所以然予用是
益以为疑愚谓朱子此言亦以一弦为宫也其意曰一
弦为宫则第三弦为角一弦之宫定为黄钟则三弦之
角必定为姑洗夫一弦为黄钟其十徽乃仲吕之位
(准焦尾至七徽之弦度合十二律吕之位如散声为黄钟则十三徽六
分为大吕十三徽一分为太蔟十二徽 )
(二分为夹钟十徽八分为姑洗十徽为仲吕九徽四分为蕤宾九徽为
林钟八徽半为夷则七徽九分为南吕 )
(七徽六分为无射七徽三分为应钟七徽亦为黄钟与散声相同也琴
止用五正声律吕得相合为用者黄钟 )
卷上 第 51a 页 WYG0220-0720c.png
(太蔟姑洗林钟南吕五声而已其馀俱不得为用故不可较以十二律
吕止以五声之数考之最为简便 不)
当应第三弦姑洗之角似与律吕相生之理不能合故
有此疑也夫以一弦全度散声为黄钟宫上生九徽之
林钟徵以应四弦散声林钟徵下生十三徽之太蔟商
以应二弦散声太蔟商上生八徽之南吕羽以应五弦
散声而南吕羽下生十一徽之姑洗角独不应三弦散
声其应三弦散声者乃在十徽之仲吕角是可疑矣殊
不知一弦实非宫分本属徵也三弦之为角分者乃宫
也惟以一弦全度散声为林钟徵上生九徽之太蔟商
卷上 第 51b 页 WYG0220-0720d.png
而应四弦散声太蔟商下生十三徽之南吕羽而应二
弦散声南吕羽上生八徽之姑洗角而应五弦散声姑
洗角下生十一徽之应钟变宫为不用之位
故不应三弦散声也应夫三弦散声者乃十徽
之黄钟宫也盖朱子以律吕之长短用三分损益之法
相较故无由得其所以然之理若以五声之位得弦度
之长短用三分损益之法相较则知一弦为徵三弦为
卷上 第 52a 页 WYG0220-0721a.png
宫而弦音与徽分皆得应和自与律吕相生之理相合
矣如弦度之十徽乃全度四分之三三分益一分而为
四分则十徽之位生全度之散声也夫五音相生宫为
声之始无声以生宫也众弦于十徽有声为用皆生散
声者也惟三弦于十徽无声为用因三弦为宫故十徽
无声以生之也此三弦为宫之至理知三弦之属宫则
知一弦六弦属徵二弦七弦属羽四弦属商五弦属角
矣一弦属徵则一弦之十一徽非姑洗角位乃应钟变
宫之位也自不应三弦散声其十徽非仲吕角位乃黄
卷上 第 52b 页 WYG0220-0721b.png
钟之宫位也自应三弦散声矣三弦属宫则三弦之十
徽乃仲吕角位自不应五弦散声其十一徽乃姑洗角
位自应五弦散声矣然则论琴者惟以弦度之长短较
以五声自然得其要而有合于管子徵羽之数大于宫
与白虎通一弦尚徵之说也今绘十二律吕合弦度之
位于左审音者辨之
卷上 第 53a 页 WYG0220-0721c.png
琴旨卷上
卷上 第 53b 页 WYG0220-0721d.png
